24.6.2025, Makkum (NL)     Logik und Mengenlehre

    Wikipedia: Logik
Mit Logik (altgriechisch: Kunst des Denkens, Kunst des Argumentierens) wird im Allgemeinen das vernuenftige Schlussfolgern und im Besonderen dessen Lehre - die Schlussfolgerungslehre oder auch Denklehre - bezeichnet. In der Logik wird die Struktur von Argumenten im Hinblick auf ihre Gueltigkeit untersucht, unabhaengig vom Inhalt der Aussagen.


Die Aussagenlogik befasst sich mit Wahrheitstabellen und Schlussregeln.




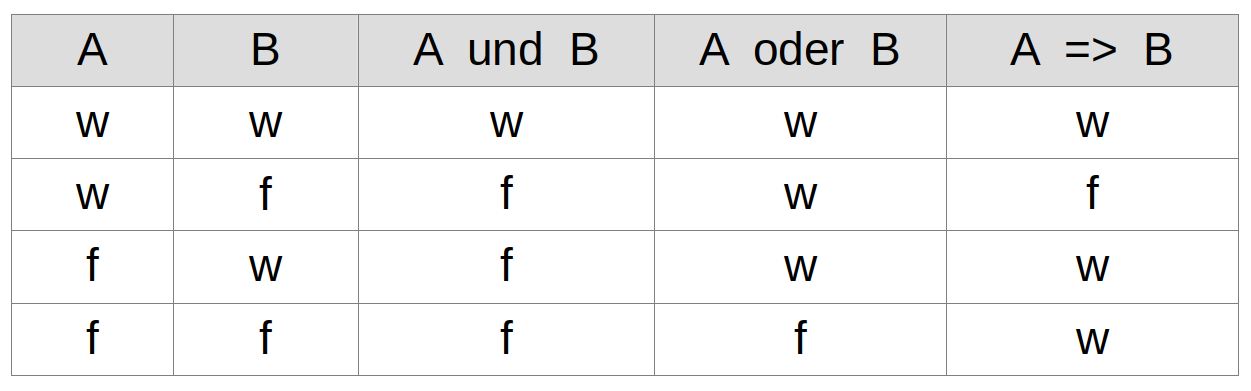
Der Modus Ponens ist eine seit der Antike gebraeuchliche Schlussregel:   A,   A  =>  B, dann   B

Der Wetterbericht sagt Windstaerke 6, in Boeen 8, voraus. Wenn der Wind sehr stark ist, kann man nicht segeln.

A : Der Wind ist sehr stark.
A  =>  B : Wenn der Wind sehr stark ist, kann man nicht segeln.
Conclusio: Heute wird nicht gesegelt.

"Heute wird nicht gesegelt" kann aber viele andere Ursachen haben. Starker Wind und nicht Segeln koennen sind nicht aequivalent.


gute und ausreichend viele finite Elmente
gutes Berechnungsprogramm
korrekte Randbedingungen
______________________________     =>     gutes Berechnungsergebnis

Der Beweis von " => " fuer eine grosse Zahl von Berechnungsaufgaben ( lineare Statik, stationaere Temperatur ) findet sich z.B. in dem Buch von Ciarlet, The Finite Element Method for Elliptic Problems, 1980.
Fuer den Beweis von " <= gilt nicht " reicht es aus, ein einziges Gegenbeispiel anzugeben.


Weitere Schlussregeln sind der Modus Tollens ( A  =>  B , nicht B, dann nicht A ) und die Kettenregel ( A  =>  B   ,   B  =>  C , dann A  =>  C ) und andere.



    Wikipedia: Mengenlehre
Die Mengenlehre ist ein grundlegendes Teilgebiet der Mathematik (altgriechisch: Kunst des Lernens ), das sich mit der Untersuchung von Mengen, also von Zusammenfassungen von Objekten, beschaeftigt. Die gesamte Mathematik, wie sie ueblicherweise gelehrt wird, ist in der Sprache der Mengenlehre formuliert und baut auf den Axiomen der Mengenlehre auf.




Georg Cantor, Bertrand Russell, Kurt Goedel

    Anwendugen der Mengenlehre

Beispiele:
    (A)   Die Menge der Ursachen fuer das Liegenbleiben im Hafen
    (B)   Die Menge der natuerlichen Zahlen
    (C)   Die Menge der Loesungen einer Berechnungsaufgabe

Georg Cantor (1845 -1918) hat die Mengenlehre begruendet. Er hat den Begriff der Unendlichkeit revolutioniert. Die Menge der natuerlichen Zalen ist unendlich. Zwei Mengen sind gleich maechtig, wenn es eine eins zu eins Abbildung zwischen ihren Elementen gibt. Das ist fuer endliche Mengen sofort einleuchtend. Fuer unendliche Mengen ( z.B. natuerliche Zahlen und gerade natuerliche Zahlen ) muss diese Abbildung angegeben werden. Fuer natuerliche Zahlen und reelle Zahlen kann keine solche Abbildung angegeben werden.



Damit sind die reellen Zahlen mehr unendlich als die natuerlichen Zahlen.

Gibt es zwischen diesen beiden Unendlichkeiten andere Unendlichkeitsstufen?

Die Antwort argumentiert modellheoretisch: So wie es verschiedene Vektorraeme zu den Vektorraum-Axiomen gibt, und es euklidische und nicht-euklidische Geometrien gibt, gibt es auch Mengenlehren mit und ohne solche Unendlichkeitsstufen. (1963, Unabhängigkeit der Kontinuumshypothese).

Schon Cantor hat die Moeglichkeiten, eine Menge zu bilden, eingeschraenkt. Bertrand Russell hat 1903 geeigt, dass die Mengenlehre ohne eine solche Einschraenkung widerspruechlich waere. Er definiert

    R = { x | x ist nicht Element von x } und fragt: ist R ein Element von R ?

Diese Erkenntnis fuehrte zur Grundlagenkrise der Mathematik. Sie erhoehte den Druck auf die Mathematiker zu beweisen, dass die Mengenlehre mit geeigneten Axiomen zur Mengenbildung widerspruchsfrei ist.

Kurt Goedels Unvollstaendigkeitssatz setzte diesen Bemuehungen 1931 ein Ende. Er bewies, dass die Widerspruchsfreiheit nicht beweisbar ist. Diese Aussage setzt auch der kuenstlichen Intelligenz Grenzen. Die Ingenieure, Forscher und Juristen von heute muessen in dieser unvollstaendigen Welt leben, in der ein neuer fundamentaler Widerspruch jederzeit auftreten kann, aber seit 1903 nicht aufgetreten ist.