Lautsch Finite Elemente GmbH was founded in 2006.

Dr. Michael Lautsch
Studies Mathematics and Logic in Muenster and Bonn, Germany.
| 1986 | Ph D about Finite Elements and Computerized Tomography. |
| 1987 - 2006 | Computer-aided engineering at Daimler AG |
| 2006 | Lautsch Finite Elemente GmbH |
| 2016 | Multigrid Marching Tetra Method |
After 19 years of CAE experience at Daimler and some deep insights into the relevant pre-, main- and post-processing software LFE started to develop its own tools. The goal is to simplify and to automize the workflow between CAD data and main processing. Sending CAD data to a country XYZ just to be meshed for a lower price should be replaced by a reliable software.
LFE spent several years to find a method which combines already meshed parts to one mesh for several parts. We failed. Mesh generation cannot be separated from combining parts. 2016 we started to build a mesher for an arbitrary number of parts.
LFE is proud to present the Multigrid Marching Tetra - MMT - software which can translate Digital Prototypes into ready to use Finite Element input data.
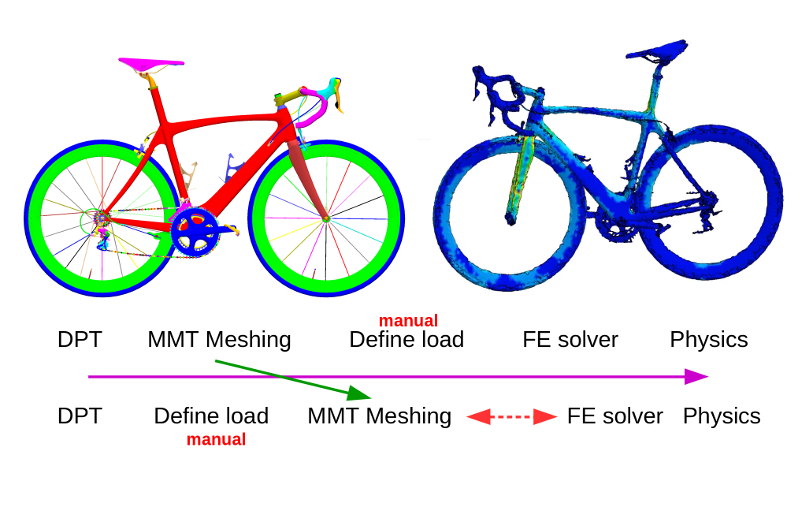
The complete definition of the solver's job before the meshing step would allow interaction between mesh generation and solver, i.e. would allow real adaptivity. This is one of LFE's future projects.
Multigrid Marching Tetra is a union of three words where each tells a story of its own.
Multigrid Methods were popular among Finite Element mathematicians between 1980 and 1990. From coarse to fine a rigid hierarchy of FE meshes was built to run the linear solver near to its minimal costs: constant * n log n where n is the number of nodes. But mesh generation was too complicated and only algebraic multigrid methods survived.
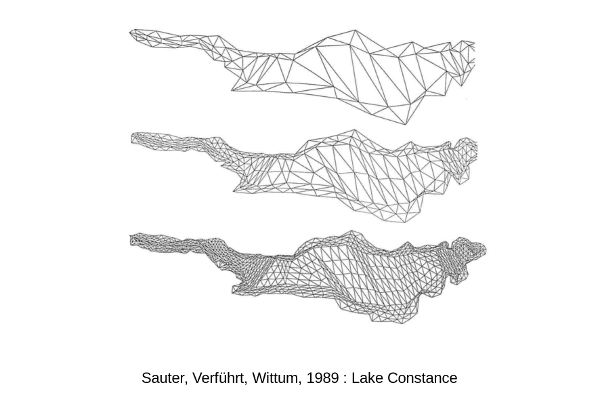
Marching Cubes is a very simple idea: Given a fine hexaedral lattice you take the cells inside a part to your mesh, cells which are hit by the boundary are split. This idea was patented in 1985 and further developements were blocked for the next 20 years.
Before 1994 tetrahedral Finite Elements had a bad reputation. 'Tetras do not work'. To create a reasonable hexaedral mesh by hand was cosidered to be good engineering work. Unfortunately this work was slow and for complicated parts took longer than the developement of the part.
In 1994 Delaunay meshing arrived at the automotive industry and started its victory: After some preliminaries automatic meshing was possible and from now on tetras did work.
The Multigrid Marching Tetra method borrows its ideas from all of these areas:
It starts on the very corsest level: A single cubic tetra covers the entire CAD-Input. From here MMT sucks to the surfaces via adaptive tetrahedral refinement. Even the classical Marching Tetra -step is a mesh refinement step.
I hope that somebody at sometime will exploit the mesh hierarchy to solve the linear system by some classical old fashioned Multigrid method and make Trottenbergs 'geometric Multigrid does not work' look as strange as 'Tetras do not work'.
Michael Lautsch, October 2021
HOME
contact michael.lautsch[at]lautsch-fe.com