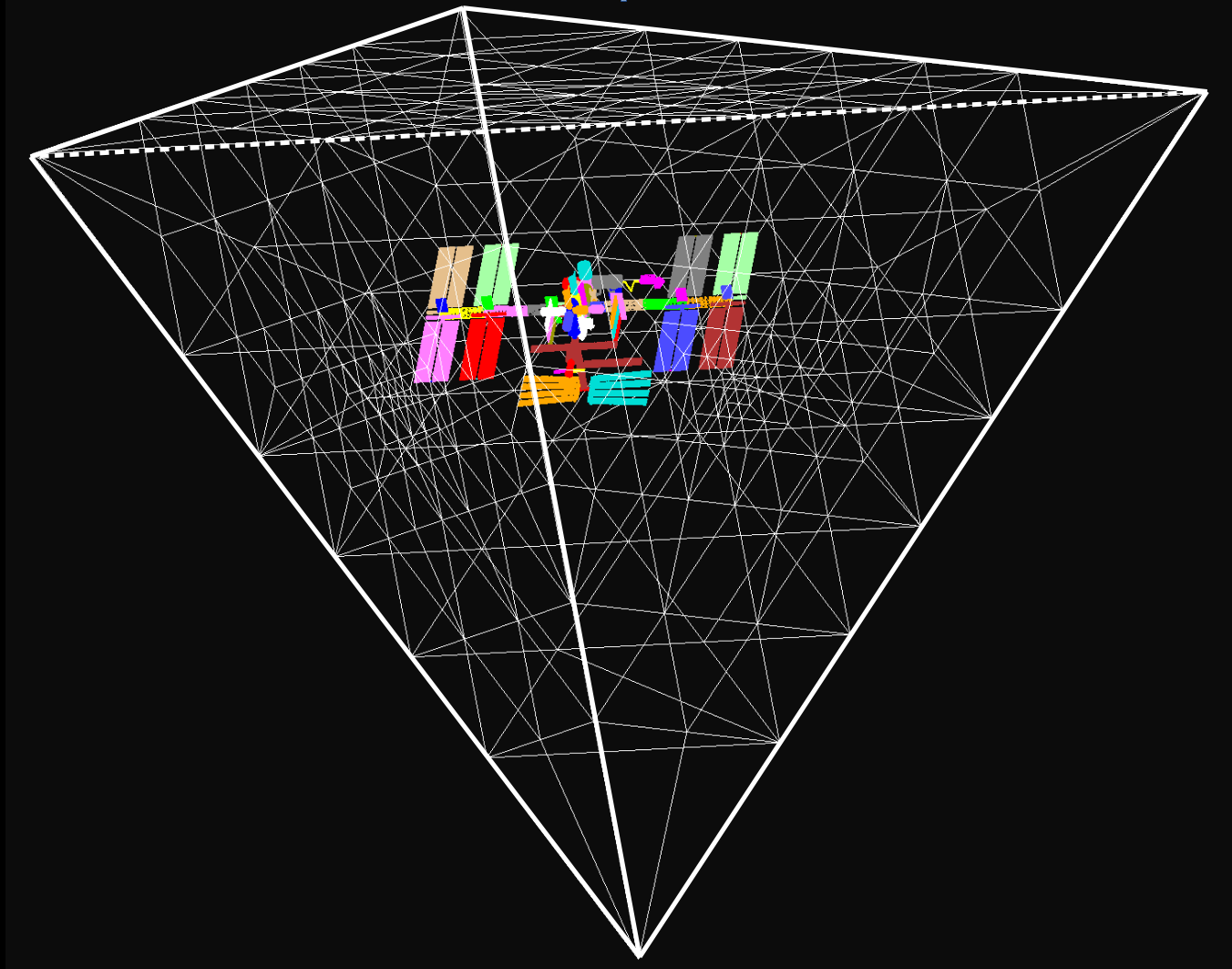
n cubic tetras self similar split of the cubic tetra LFE Logo made in Italy at puntomarmoepietre.it International Space Station made from prisms marble tetras Body centered and cubic - the Atomium in Brussels from this it is easy to see that the volume of the cubic Tetra = 1/12 Covering three-dimensional space with tetrahedra is one of the oldest questions in mathematics. It is said that Aristotle (384 - 322 B.C.) claims that space could be covered with regular tetrahedra without gaps and it was Regiomontanus (1436-1476 A.D.) who realized that this was not correct. The proof is simple: 3, 4, 5 or 6 tetrahedra must come together at each edge without gaps. But this is not possible. Hill (1896), Sommerville (1923), Baumgartner (1968) and Goldberg (1972) have specified 5 different tetrahedra which tile 3D space. The most striking of which is our cubic tetra. If you divide the cubic tetra at the longer edge into 2 equal ones, you get the 2nd from the list of 5. By further divisions you get the 3rd and the 4th . Our cubic tetrahedron has the best element quality of these 5. Or is there still the great unknown? The list of tetras is not complete. New mathematical results show that there are none. HOME contact michael.lautsch[at]lautsch-fe.com