MULTIGRID MARCHING TETRA ALGORITHM Two different refinements: BCC: Starting from a single tetra the Body Centered Cubic Grid is refined adaptively. A BCC-tetra is octree refined if the MT-refinement would not interpolate the geometry well. MT: If the final Marching Tetra refinement does not work well it simplifys the geometric setting.     Tetra element quality     Why tetras ?     Why hexas ?       BCC is Delaunay and Voronoi     Marching Cubes and Marching Tetras     10 000 parts     Geometry engine     ADAPTIVE     Multigrid Marching Tetra     Multigrid 1990     A * x = b   for the price of   A * b = x ___ Tetra element quality The normalised volume is chosen as a measure for the quality of a tetra. The quality of the regular tetra is 1.0 . Element quality   =   6 * sqrt 2 * Volume / (max edge length)**3 . ___ Why tetras ? Tetras are simpler than hexas. ___ Why hexas ? 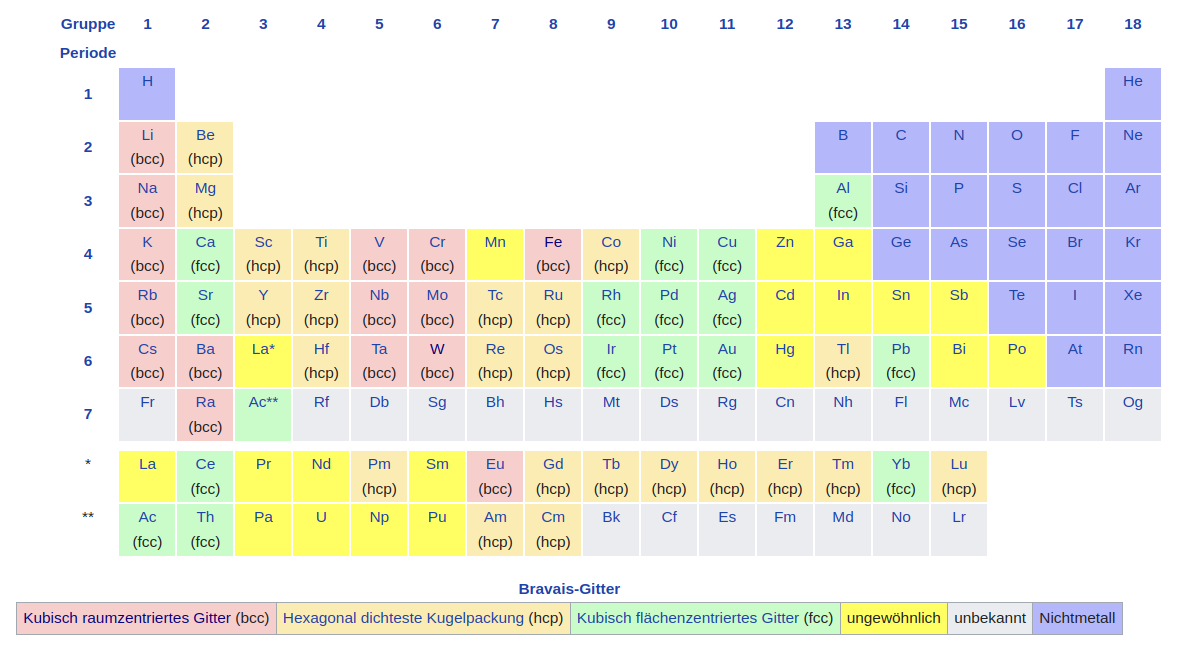The Body Centered Cubic ( BCC ) grid is the most popular distribution of points in 3D space. It is simply the standard cubic grid plus a (0.5, 0.5, 0.5) translated copy. The Atomium at Bruxelles celebrates the basic cell of the BCC grid. 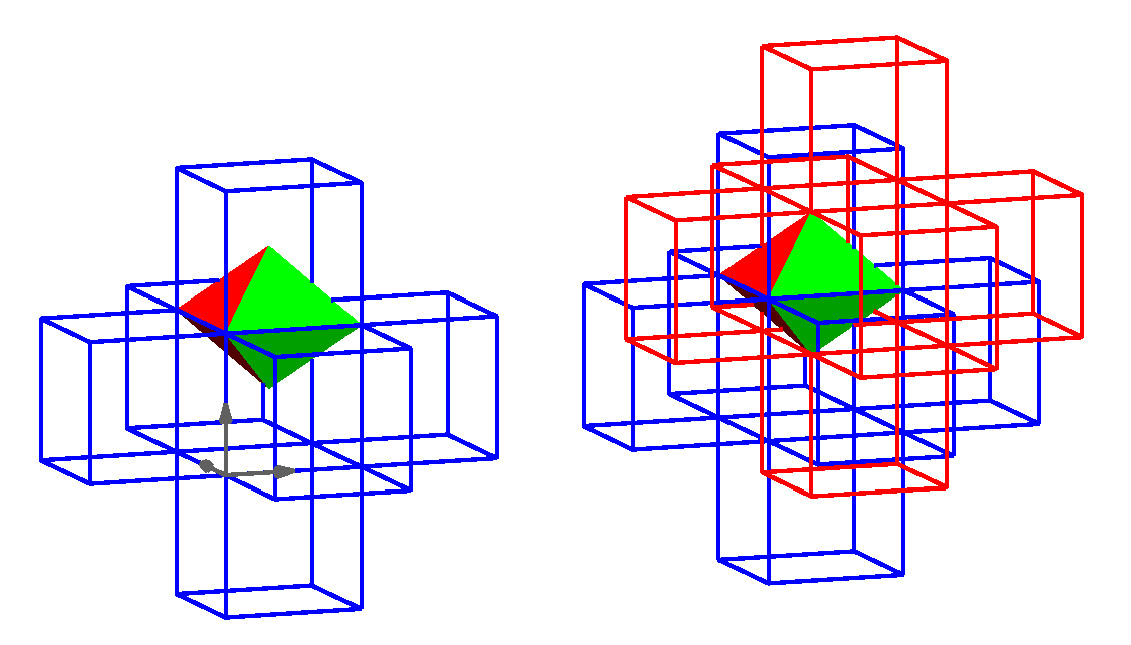___ BCC is Delaunay and Voronoi an octahedron and the cubic / BCC grid gb The space between the points of the BCC grid can be filled with octahedrons (BCC-octa). These octahedrons are a Voronoi tiling of the 3D space. The center of the Voronoi cell is the crossing point of the three diagonals of the BCC-octa. The octas can be split along the shortest diagonal into 4 "cubic" tetras (BCC-tetra). The BCC-tetra mesh is Delaunay: The center of the Ball which carries the 4 points of the cubic tetra is the mid of the mids of the two longer edges. Inside this ball is no BCC grid point. BUT: BCC-tetra and BCC-octa are not dual in the Delaunay Voronoi sense. This can be seen by the distribution of the cicumspheres of the BCC-tetras and by the location of the centers of the BCC-octas. The cubic tetra can be split selfsimilarly into 8 smaller ones. This allows tetrahedral octree meshing. Repeated octree meshing of the cubic tetra creates the BCC-tetra mesh. The nodes of a locally refined mesh are a subset of a fine BCC grid. The quality of the cubic tetra is   0.5 * sqrt ( 2.0 ) Element quality of the transition tetras   >   0.15 ___ Marching Cubes and Marching Tetras Marching Cubes were introduced 1991 to visualize CT scan data. The algorithm works for a cubic tiling as it works for a tetra tiling. Assume the scan data are continuous and let the data be given at the gridpoints. We want to find the iso surface where all scan data carry the same density, say α . For each edge with density at point_0   >   α and density at point_1   <  α find the α point. Interpolate these points on the cubic or tetra tiling. This idea is transferred to mesh generation: Let point_0 belong to part A and point_1 not belong to part A. If there is one crossing of the   point_0 to point_1   edge and the surface of part A, the edge is cut there for the MT mesh. If there are more crossings: If BCC edge refinement is allowed we do so, otherwise we locally simplify the surface of part A by creating an artificial single surface point. ___ 10 000 parts temperature of a V engine       ____ what is a part? STL file, watertight triangular surface, no free edges, no T joints       ____ incorrect surface some simple automatic improvement tools run after starting MMT. barycentric limits ... damage part surface ...       ____ 10 000 parts, Boolean operations, mesh simplification, recursive geometry hierarchy of parts, last part wins, first part = fluid ___ Geometry engine BCC mesh: The geometry engine computes location and normal of all intersecions of a BCC edge with all parts. New BCC edges are either coincident with elder ones or start and finish on elder ones.       ____ part boundaries are not allowed to cross elements of the final mesh. Nodes may belong to different parts, as well as edges. Tria and quad elements may belong to two parts, volumes to just one part.       ____ edge bisection or simplification A BCC edge with different part associations at its nodes must have at least one crossing with the part surface. Multiple crossings are resolved by edge refinement when refinement is allowed, otherwise a midnode is generated. Single crossings are the source of triangle splits and tetra splits of the MT mesh.       ____ edge trisection or simplification A BCC edge with the same part associations at its nodes may have no crossing or an even number of crossings with the part surface. 4 and more crossings are resolved by edge refinement when refinement is allowed, otherwise the edge is not split. 2 crossings are the source of triangle splits and tetra splits of the MT mesh.       ____ corners or simplification corners are computed by using the normals at the intersection points. If the corner is inside ( triangle or tetra ) the triangle / tetra split is performed with this corner. Otherwise the split is performed without this corner.       ____ worst element   >   1.e-7 barycentric limits       ____ MMT refinement terminates for simple parts. long part edges via trisection of BCC edges. But no answer for corners.       ____ organization of geometry Octree storage of the nodes of the STL input has to follow the BCC refinements. Up to now an unused option.       ____ STL edges vs. BCC triangles For now an unused option ___ ADAPTIVE my personal story accuracy requirements of the PDE, error criteria ... geometric needs: refine edges, when ... , refine triangles, when ... refine tetras, when ... ... are iterative processes, which play together ... 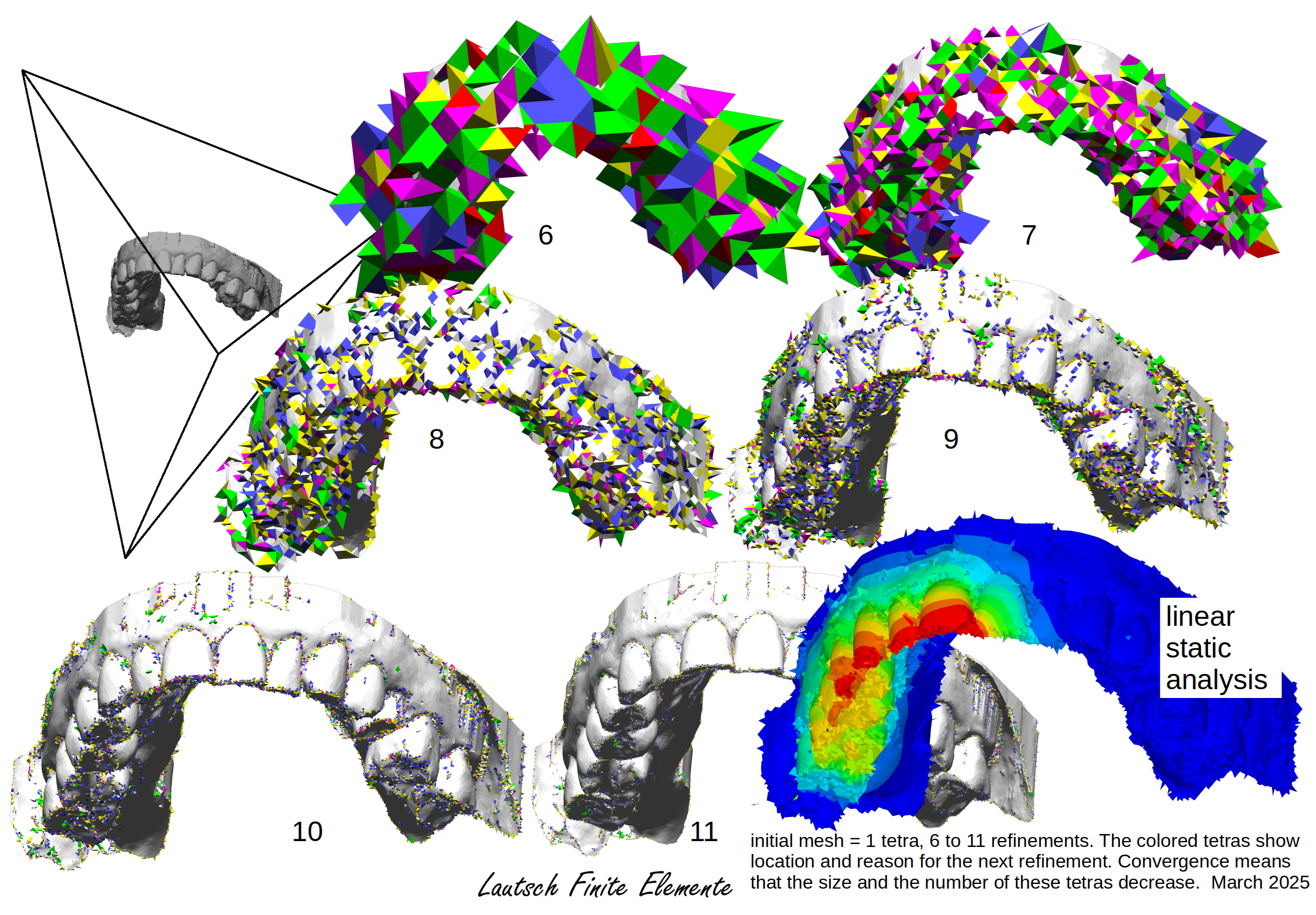___ Multigrid Marching Tetra detail       A single tetra covers the solid part (upper jaw of M. Lautsch). Edges, triangles and tetras are refined, when they cannot represent the boundary. This process terminates when the part is reconstructed correctly or smooth approximations can be tolerated. How bad can the worst element be? Do we need mesh improvement as a very last step? 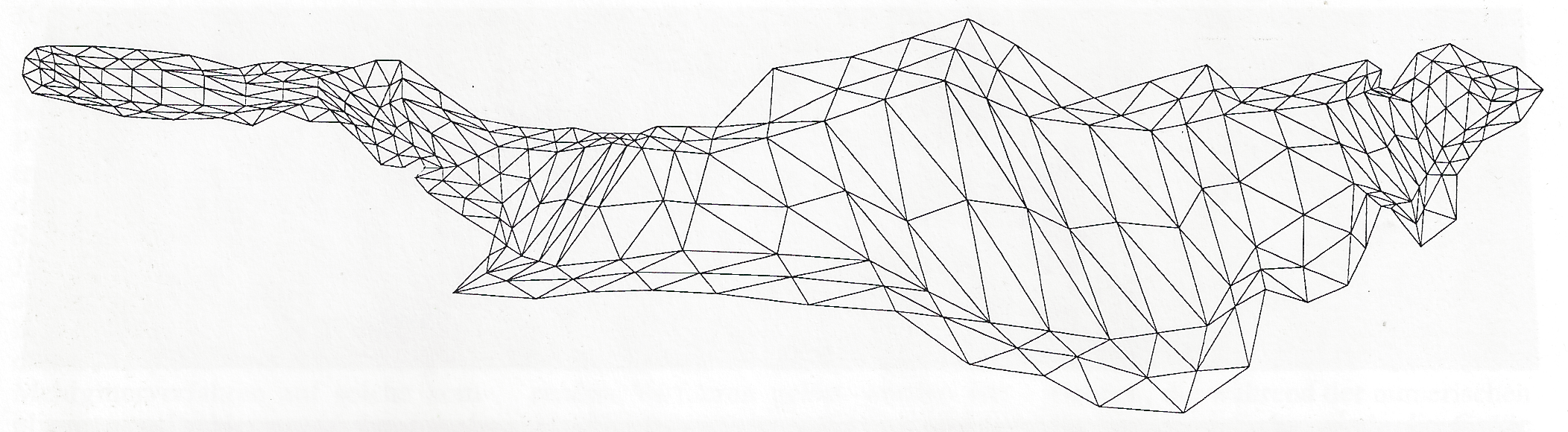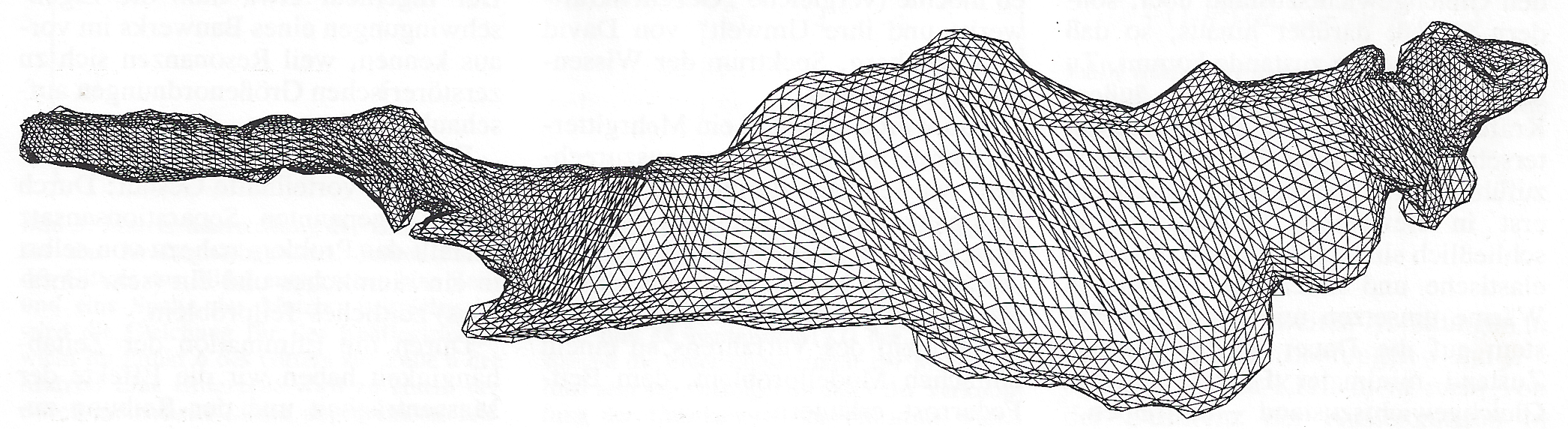___ Multigrid 1990     A * x = b   for the price of   A * b = x level 0 level 1 level 4 Multigrid Methods were very famous from 1985 until 1995. The idea was to solve the linear system which arises from Finite Element discretization as fast as possible. Given the stiffness matrix A and a vector b , computing   x = A * b   takes   constant * N   operations, N is the number of nodes. This is the lower bound of the number of operations for computing the inverse :   A * x = b . An explicit time step in dynamic analysis takes constant * N operatons, but the number of time steps is huge. Implicit time steps may be much larger. Direct (Gaussian) Methods take   constant * N**q   Operations and q > 1.0 THE QUESTION IS: IS THERE ANY OPTIMAL METHOD ? THE ANSWER IS: YES but there are two restrictions: first: instead of constant * N we have constant * N * log N Operations. But log N increases slowly. second: We have to use special FE spaces: Nested, hierarchical, Multigrid. The optimal method was applied to a nice Problem - tsunami at lake constance - and published for everybody in "Spektrum der Wissenschaft", a higher level of attention is not possible. Since 1994 automatic meshing by Delaunay's Method became popular. But these meshes do not fit to the requirements of the FE spaces for the OPTIMAL METHOD. In 2002 the first BCC meshes came into the discussion of mesh generation methods. These FE spaces are nested, hierarchical, Multigrid. They distinguish from the traditional Multigrid meshing idea in one point: Part boundaries are fixed in the last refinement step. Now I ask: MMT is named "Multigrid". Is this algorithm Multigrid in the 1990 fashion? TOP HOME contact michael.lautsch[at]lautsch-fe.com